close Home Motivation Flow Map Movements Distances Services Method Tools Team

Visualizing Healthcare Accessibility in Singapore

Let's start the exploration!

Motivation

Background

As one of the most densely populated countries in the world, Singapore faces challenges in ensuring equal access to healthcare for all. The high population density has increased the demand for healthcare services, putting strain on the country's medical infrastructure. Although clinics are located in every neighborhood, the quality and intensity of healthcare services vary in different parts of the city-state, leading to disparities in access. Additionally, healthcare services in different geographic areas may experience varying levels of demand, subsequently affecting their ability to provide high-quality care to patients. It is thus critical to assess the spatial distribution of the availability and accessibility of healthcare services.

Problem

The spatial distribution of the availability and accessibility of healthcare services requires more exploration and analysis.

Solution

This project presents a framework to measure the healthcare intensity by combining two popular models: radiation models and 2-step floating catchment area (2SFCA). More information about the two models is described in the Method section.

Visualization

After the flows were estimated and healthcare intensity were calculated, we show the results below in 4 sections:
  1. Flow Estimation Map
  2. Movements between Planning Area
  3. Distribution of Travel Distances
  4. Service Intensity Map
The first map.

Flow Estimation

The widths of arrows indicate the flow size. The size of circles show the total incoming/outgoing flows. Dark circles: more outgoing, bright circles with inner ring: more incoming, bright circles: almost same. Click here for full-page map and more exploration at different scales. Detailed inter-hexagon flows were shown as tooltips in the full-page map. Yellow color lines show the relatively lower flows, which could be observe in the full-page map.

See the flows aggregated by towns.

Movements between towns

The alluvial graph show the estimated flows between each town to seek for clinics. The colors indicate the region of the towns (blue: Central Region, green: East Region, grey: North Region, red: North-East Region, orange: West Region). Most of the same-towns and same colors conncetions are thick, indicating most of the people move locally for accessing healthcare services. More thin cross-regions/cross-towns lines occurr in blue highlighting that the movements for people living in Central Region are more complex. Click here for full-page plot.

How does the travel distances distributed?

Travel Distance

The chart shows the distribution of travel distances for the people living in the five regions of Singapore. The chart highlighted the longer travel distances could be made by people living in the Central Region compared to the other four regions. Click here for full-page plot.

The main result map.

Service Intensity

The received service intensities are calculated based on a 2SFCA approach. The colors of the underlying hexagon cells show the total incoming flows to each hexagon cell (with at least 1 clinic): darker indicates more incoming flows. The size and colors of circles indicate the healthcare intensities: larger and darker indicates stronger intensity. Click here for full page map.

The methods.

Methodology

Full page image.

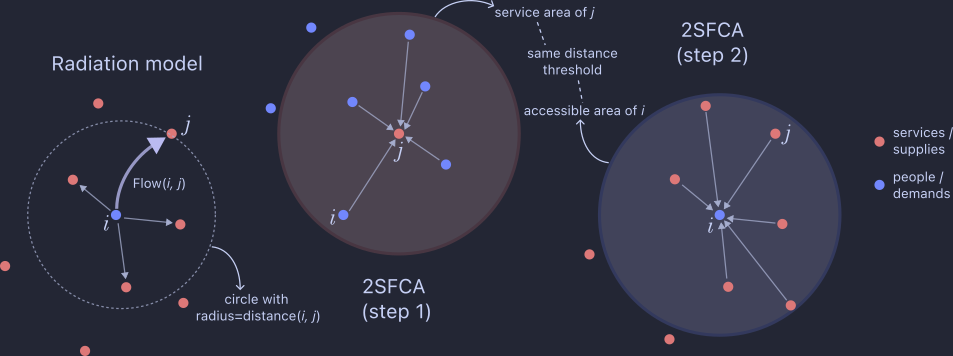
Two main concepts were used in this project: radiation model (Simini et al., 2012) and two-steps floating catchment area (2SFCA, Luo and Wang, 2003). The chart above provides a brief demonstration of the two concepts. The flow between \(i\) and \(j\) is calculated using: $${\langle T_{ij} \rangle = T_i \times \frac{m_i n_j}{(m_i+s_{ij})(m_i+n_j+s_{ij})}}.$$ The service-to-population is calculated using: $${R_j = \frac{N_j}{\sum_{k\in SA_j} P_k }}$$ and the accessibility is then calculated by using: $${A_i = \sum_{j \in S_i} R_j}.$$ The models were adapted based on our analysis setting.

The tools and team.

Data Sources & tools

Data sources

Processing and Analysis

  • QGIS: hexagon generation
  • Pandas: data processing & calculation
  • GeoPandas: geometry & projection
  • OSMNX: routing & distance calculation

Visualization

Web design & hosting

The Team

Wei Chien Benny CHIN
Research Fellow
Chen-Chieh FENG
Associate Professor
Yi-Chen WANG
Associate Professor

GIS Unit, Department of Geography, National University of Singapore